Wolfram|Alpha es capaz de resolver una amplia variedad de sistemas de ecuaciones. Puede resolver sistemas de ecuaciones lineales o sistemas que involucren ecuaciones no lineales, así como buscar específicamente soluciones enteras o soluciones sobre otro dominio. Además, puede resolver sistemas que involucren desigualdades y restricciones más generales.
Solucionador de sistemas de ecuaciones en línea
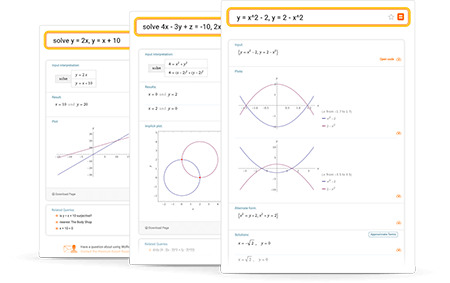
Resuelva ecuaciones y sistemas de ecuaciones mediante Wolfram|Alpha
Una útil herramienta para encontrar soluciones para sistemas de ecuaciones y restricciones
Aprenda más
Consejos para ingresar consultas
Ingrese sus preguntas utilizando español simple. Para evitar preguntas ambiguas, asegúrese de usar paréntesis según sea necesario. Estos son algunos ejemplos que ilustran preguntas sobre cómo resolver sistemas de ecuaciones.
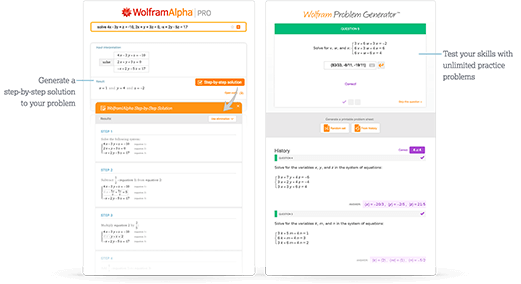
Acceda de forma inmediata a herramientas de aprendizaje
Obtenga de forma inmediata comentarios y guías con soluciones paso a paso y Wolfram Problem Generator
Aprenda más
¿Qué son los sistemas de ecuaciones?
Un sistema de ecuaciones es un conjunto de una o más ecuaciones que involucren un número de variables.
Las soluciones para sistemas de ecuaciones son los mapeos de variables de manera que todas las ecuaciones componentes estén satisfechas, es decir, las ubicaciones en las cuales todas estas ecuaciones se cruzan. Resolver un sistema implica encontrar todas estas soluciones comunes o puntos de intersección.
Los sistemas de ecuaciones lineales son un subconjunto común y aplicable de sistemas de ecuaciones. En el caso de dos o más variables, estos sistemas pueden considerarse como líneas dibujadas dentro del espacio bidimensional. Si todas las líneas convergen en un punto en común, se considera que el sistema es consistente y tiene una solución en este punto de intersección. De lo contrario el sistema es considerado inconsistente, ya que no tiene soluciones. Los sistemas de ecuaciones lineales que involucren más de dos variables funcionan de manera similar, ya que tienen una solución, no tienen soluciones, o tienen soluciones infinitas (este último en caso todas las ecuaciones componentes sean equivalentes).
También son posibles los sistemas más generales que involucren funciones no lineales. Estos poseen conjuntos de soluciones más complejos que involucran una, cero, infinitas o cualquier otro número de soluciones, pero funcionan de manera similar a los sistemas lineales en el sentido que sus soluciones son los puntos que satisfacen a todas las ecuaciones involucradas. También son posibles sistemas más generales de restricciones, como los que involucran desigualdades, o que requieren que ciertas variables sean enteros.
Resolver sistemas de ecuaciones es una idea muy general e importante, y es fundamental en muchas áreas de las matemáticas, la ingeniería y la ciencia.