Wolfram|Alpha es una gran herramienta para calcular derivadas de primer, segundo y tercer grado; derivadas en un punto; y derivadas parciales. Aprenda acerca de qué son derivadas y cómo las calcula Wolfram|Alpha.
WolframAlpha
Calculadora de derivadas en línea
Resuelva derivadas con Wolfram|Alpha
Más que un simple solucionador de derivadas en línea
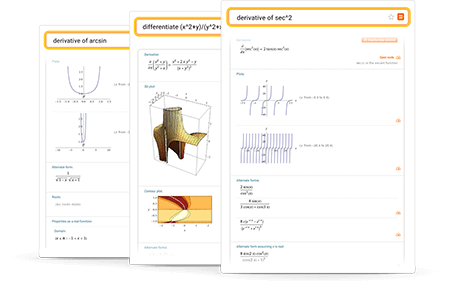
Aprenda más
Consejos para ingresar consultas
Ingrese sus consultas utilizando inglés simple. Para evitar consultas ambiguas, asegúrese de usar paréntesis cuando sea necesario. Aquí hay algunos ejemplos que ilustran cómo preguntar por una derivada.
Acceda de forma inmediata a herramientas de aprendizaje
Obtenga de forma inmediata comentarios y guías con soluciones paso a paso y el Generador de Problemas Wolfram
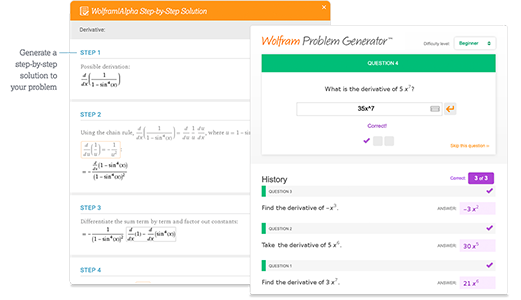
Aprenda más
¿Qué son derivadas?
La derivación es una herramienta importante en cálculo que representa el índice de cambio infinitesimal en una función en relación con sus variables.
Dada una función f x, hay varias formas de denotar la derivada de f con respecto a x. Las formas más comunes son d fd x y f'x. Cuando una derivada se toma n veces, la notación dn fdxn o fnx es utilizada. Estas son llamadas derivadas de orden superior. Note que por derivadas de segundo orden, la notación f''x es usualmente utilizada.
En un punto x = a, la derivada se define como f'a = limh0f a + h - f hh . Este límite no se garantiza que exista, pero si existe, f x se dice que es diferenciable en x = a. Geométricamente hablando, f'a es la pendiente de la recta tangente de f x en x = a.
Como ejemplo, si f x = x3, entonces f'x = limh0h+x3-x3h = 3x2 y luego podemos calcular f''x: f''x = limh03x+h2-3 x2h = 6x. La derivada es una potente herramienta con muchas aplicaciones. Por ejemplo, se utiliza para encontrar extremos locales/globales, encontrar puntos de inflexión, resolver problemas de optimización, y describir el movimiento de los objetos.
¿Cómo se calculan derivadas en Wolfram|Alpha?
Wolfram|Alpha llama a la función de Mathematica D, la cual usa la tabla de identidades más grandes que uno encontraría en un texto de cálculo estándar. Usa reglas "well known" tales como la linearidad de la derivada, regla de producto, regla de poder, regla de cadena, etc. Además, D usa reglas "lesser known" para calcular la derivada de un amplio arreglo de funciones especiales. Para derivadas de orden superior, ciertas reglas tales como la regla de producto general de Leibniz puede acelerar cálculos.