Wolfram|Alpha es una gran herramienta para encontrar raíces de polinomios y resolver sistemas de ecuaciones. Además factoriza polinomios y representa gráficamente conjuntos de soluciones de polinomios, desigualdades y más.
Solucionador de ecuaciones en línea
Resuelva sistemas de ecuaciones lineales, cuadráticos y polinomiales mediante Wolfram|Alpha
Más que solo un solucionador de ecuaciones en línea
Aprenda más
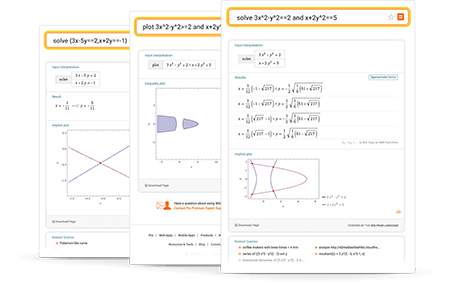
Consejos para ingresar consultas
Ingrese sus preguntas utilizando español simple. Para evitar preguntas ambiguas, asegúrese de usar paréntesis según sea necesario. Estos son algunos ejemplos que ilustran cómo formular preguntas.
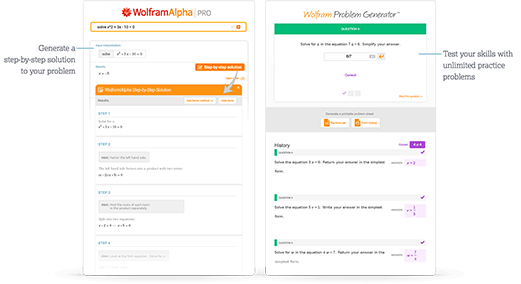
Acceda de forma inmediata a herramientas de aprendizaje
Obtenga de forma inmediata comentarios y guías con soluciones paso a paso y Wolfram Problem Generator
Aprenda más
Acerca de cómo resolver ecuaciones
Dado un valor c como raíz de un polinomio px si pc=0.
El mayor exponente de x que aparece en px se conoce como el grado de p. Si px tiene grado n, entonces se conoce que hay n raíces, teniendo en cuenta la multiplicidad. Para comprender el significado de multiplicidad, tome por ejemplo x2 - 6x + 9=x-32=x-3x-3. Se considera que este polinomio tiene dos raíces, ambas iguales a 3.
Usualmente se aprende sobre el "teorema del factor" en un segundo curso de álgebra, como una manera de encontrar todas las raíces que sean números racionales. Además se aprende cómo encontrar raíces de todos los polinomios cuadráticos usando raíces cuadradas (procedentes del discriminante) cuando sea necesario. Existen fórmulas más avanzadas para expresar las raíces de polinomios cúbicos y cuárticos, al igual que una cantidad de métodos numéricos para aproximar raíces de polinomios arbitrarios. Estos usan métodos desde el análisis complejo hasta algoritmos numéricos sofisticados, y por supuesto, esta es un área de investigación y desarrollo continuo.
Los sistemas de ecuaciones lineales a menudo se resuelven mediante eliminación gaussiana o métodos relacionados. Esto también es visto usualmente en planes de estudios matemáticos secundarios o universitarios. Se necesitan métodos más avanzados para encontrar raíces de sistemas simultáneos de ecuaciones no lineales. Lo mismo puede decirse al trabajar con sistemas de desigualdades: el caso lineal puede manejarse usando métodos cubiertos en cursos de álgebra lineal, mientras que los sistemas de polinomios de grado más alto usualmente requieren herramientas computacionales más sofisticadas.
Cómo Wolfram|Alpha resuelve ecuaciones
Para resolver ecuaciones, Wolfram|Alpha llama a las funciones Solve y Reduce de Wolfram Language, las cuales contienen un amplio rango de métodos para todo tipo de álgebra, desde ecuaciones lineales y cuadráticas básicas hasta sistemas no lineales multivariados. En algunos casos se usan los métodos de álgebra lineal, como la eliminación gaussiana, con optimizaciones para aumentar la velocidad y confiabilidad. Otras operaciones utilizan teoremas y algoritmos de teoría de números, álgebra abstracta y otros campos avanzados para calcular resultados. Estos métodos son diseñados y seleccionados cuidadosamente para permitir a Wolfram|Alpha resolver la mayor variedad de problemas, y a la vez minimizar el tiempo de cálculo.
Si bien esos métodos son útiles para obtener soluciones directas, también es importante para el sistema comprender cómo un ser humano resolvería el mismo problema. Como resultado, Wolfram|Alpha también posee algoritmos individuales para mostrar operaciones algebraicas paso a paso usando técnicas clásicas fáciles que las personas pueden reconocer y seguir. Estas incluyen eliminación, sustitución, la fórmula cuadrática, la regla de Cramer y muchas más.