Wolfram|Alpha es una potente herramienta para calcular antiderivadas e integrales definidas, integrales dobles y triples, e integrales impropias. También muestra representaciones gráficas, formas alternas, y otra información relevante para mejorar su intuición matemática.
Calculadora de integrales en línea
Resuelva integrales con Wolfram|Alpha
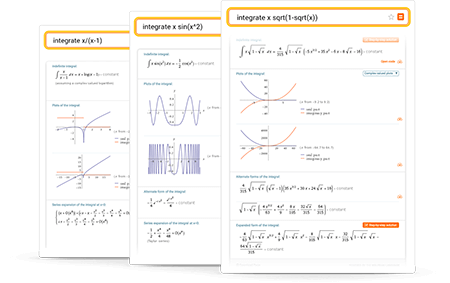
Más que un simple solucionador de integrales en línea
Aprenda más
Consejos para ingresar consultas
Ingrese sus consultas usando inglés simple. Para evitar consultas ambiguas, asegúrese de usar paréntesis cuando sea necesario. Aquí hay algunos ejemplos que ilustran cómo preguntar por una integral.
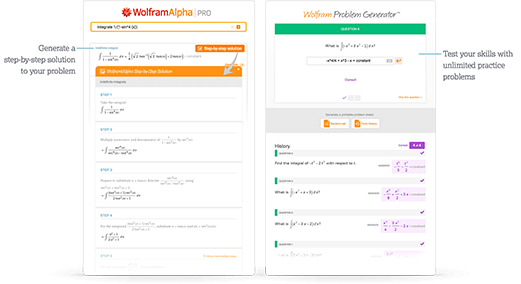
Acceda de forma inmediata a herramientas de aprendizaje
Obtenga de forma inmediata comentarios y guías con soluciones paso a paso y Wolfram Problem Generator
Aprenda más
¿Qué son las integrales?
La integración es una herramienta importante en cálculo ya que puede darle una antiderivada o puede representar el área en una curva.
La integral indefinida de f(x), denotada como ∫f(x) dx, es definida como la antiderivada de f(x). En otras palabras, la derivada de ∫f(x) dx es f(x). Dado que la derivada de una constante es cero, las integrales indefinidas son definidas solamente hasta una constante arbitraria. Por ejemplo, ∫sen(x) dx=−cos(x)+constante, dado que la derivada de −cos(x)+constante es sen(x). La integral definida de f(x) desde x=a hasta x=b, denotada como ∫baf(x) dx, es definida como el área determinada entre f(x) y el eje x, desde x=a y x=b.
Ambos tipos de integrales están unidos por un teorema fundamental de cálculo. Este indica que si f(x) es integrable en [a,b] y F(x) es su integral indefinida continua, luego ∫baf(x) dx=F(b)−F(a). Esto significa que ∫π0sen(x) dx=(−cos(π))−(−cos(0))=2. Algunas veces una aproximación a una integral definida es deseada. Otra forma común de hacer esto es colocando rectángulos delgados bajo la curva y agregando las áreas determinadas juntas. Wolfram|Alpha puede resolver un amplio rango de integrales.
¿Cómo se calculan integrales en Wolfram|Alpha?
Wolfram|Alpha calcula integrales de forma distinta que las personas. Llama a la función Integrate de Mathematica, la cual representa una enorme cantidad de investigación matemática y computacional. Integrate no realiza el cálculo de integrales como las personas. En su lugar, utiliza algoritmos potente y generales que usualmente involucran operaciones matemáticas sofisticadas. Existen dos enfoques que comúnmente se consideran. Uno consiste en trabajar la forma general de una integral, luego diferenciar esta forma y resolver ecuaciones para que coincida con los parámetros simbólicos indeterminados. Incluso para los integrandos simples, las ecuaciones generadas de esta forma pueden ser altamente complejas y requieren de las potentes capacidades algorítmicas de Mathematica para resolverlas. Otro enfoque que Mathematica utiliza para trabajar con integrales, es convirtiéndolas en funciones hipergeométricas generalizadas, entonces utiliza colecciones de relaciones acerca de estas funciones matemáticas altamente generales.
Mientras que estos potentes algoritmos le dan a Wolfram|Alpha la habilidad de computar integrales rápidamente y de manejar un amplio arreglo de funciones especiales, comprender cómo un humano integraría también es importante. Como resultado, Wolfram|Alpha también tiene algoritmos para realizar integraciones paso a paso. Éstas usan técnicas de integración completamente diferentes que emulan la forma en que los humanos se acercarían a una integral. Esto incluye la integración por sustitución, la integración por partes, la sustitución trigonométrica y la integración por fracciones parciales.